IT/모바일
제공 : 한빛 네트워크
저자 : George T. Heineman
역자 : 한빛독자
원문 : December Column: Searching Algorithms
이 컬럼은 2008년 10월 오라일리에서 출간한 Algorithms in a Nutshell 관련 블로그에 연재된 월간 컬럼 시리즈의 두 번째 기사다.
지난 컬럼에서는 다음 내용을 다뤘다.
12월 컬럼의 코드 샘플 다운로드
코드 샘플인 code.zip 파일(141,995바이트)은 이곳에서 다운 로드받을 수 있다. 예제는 윈도우에서 이클립스 3.4.1 버전으로 테스트하였고 JDK 버전은 1.6.0_05이다. code.zip 파일은 익스포트된 이클립스 프로젝트기 때문에 이클립스 워크스페이스로 쉽게 불러올 수 있다. 이클립스 외부에서 컴파일하고 실행하려면, CLASSPATH 환경 변수를 설정하여 컴파일된 ADK 소스를 사용하게 하면 된다.
코드를 이클립스로 임포트하는 방법은 컬럼 뒷부분을 참고하기 바란다.
검색 루틴용 API 인터페이스
다음 코드는 원소 집합에 특정 원소가 존재하는지 여부를 판단하는 API(이 블로그용으로 정의함)를 보여준다.
구체적으로 표현하기 위해 검색할 대상 집합의 크기를 n이라고 한다. n개의 원소 각각의 키(key) 값을 계산할 수 있는데, 해시 기반 집합에서는 b개 저장소(슬 롯이라고도 한다)의 배열을 만든다.
순차 검색: 다소 아쉬운 알고리즘
해싱 연구의 목적은 순차 검색의 약점을 극복하기 위함이다. 집합이 정렬되어 있지 않으면 한 원소를 검색하는 데 최악의 경우 O(n)의 비용이 든다. 집합이 정 렬되어 있어도 원소가 고르게 배분되어 있으면 원소의 절반을 조사해야 하므로 비용은 여전히 O(n)이다.
해시 기반 검색: 선형 탐색
선형 탐색은 본질적으로 적은 탐색 횟수만으로 배열에 특정 원소가 존재하는지 여부를 판단할 수 있는 배열을 통해 집합 원소를 분산시킨다. 이를 위한 첫 번 째 방법은 b(저장소의 개수)가 n(원소의 개수)보다 클 수 있음을 인식하는 것이다. 해시 함수가 원소를 저장할 저장소를 계산하기 위해 원소의 키 값을 받고 보 통 나머지 연산자("%")를 사용해 b개 저장소 중 하나에 맞게 정규화한다. 정규화한 저장소 번호는 h라고 한다. 두 번째 방법은 계산된 저장소가 같은 원소가 둘 이상일 때 충돌을 해결하는 것이다. 선형 탐색(linear probing) 기법은 충돌을 해결하기 위해 열린 위치 지정(open addressing)을 사용하는데, 이는 insert(e) 메 소드에서 다른 저장소를 선택해 삽입 항목을 넣음을 의미한다. exists(e) 메소드는 이후에 대상 원소가 집합에 있는지 판단하기 위해 여러 저장소를 조사할 수 도 있다.
다음 메소드(첨부 코드에 있는 HashBasedSearch 클래스에서 발췌함)는 해시 테이블을 표현하는 배열에 원소를 삽입하는 로직이다. 빈 저장소를 찾는 데 탐색 한 횟수를 반환하며, 빈 저장소가 없으면 RuntimeException을 던진다. b가 소수(prime number)면, [1, b-1] 범위에 있는 모든 델타(delta)를 사용할 수 있다. 그 렇지 않으면 b와 delta의 최대 공약수(GCD, greatest common divisor), 즉 서로 소 값을 사용해야 한다.
다음 표는 delta 값을 1로 유지하고, keys2에 해당하는 641개 문자열을 크기가 서로 다른 해시 테이블에 삽입한 결과다.
저장소의 개수 b가 n에 가까워질수록 충돌 횟수가 증가한다. 213,557개 단어를 모두 조회하는 데 필요한 평균 시간을 계산하는 마지막 열에서 두드러진 현상 을 볼 수 있다. 평균 탐색 횟수가 적을 때는 O(n)의 탐색 횟수가 필요한 원소도 있어 사용자가 충분히 큰 배열을 사용해 일부 상황을 제어할 수 있다.
delta 값의 선택은 중요하지 않다. 4가지 특정 크기 배열에 서로 다른 delta 값을 적용한 결과를 보여주는 다음 표를 살펴보자.
필자는 예상보다 약 4-8배 큰 배열을 선택할 것을 권한다. 크기가 그 정도는 되어야 총 탐색 횟수는 물론 각 항목을 찾는 데 사용되는 탐색 횟수의 변화가 줄기 때문이다. 해시 테이블 배열을 만들고 나면, 배열 안에서 최대 체인이 원소의 존재 여부를 평가하는 데 드는 시간을 결정한다. 여기서는 탐색 횟수를 줄이기 위 해 여분의 (사용하지 않은) 공간을 두는 트레이드 오프가 있다.
해시 기반 검색: 2차원 탐색
2차원 탐색은 선형 탐색을 사용할 때 발생하는 클러스터링을 피하려고 시도한다. 2차원 탐색은 ((int)(hash + c1*p + c2*p*p)) % tableSize 형태의 수식을 사용 해서 p번째 저장소를 계산한다(여기서 c1과 c2는 부동소수점 계수다). 이 컬럼의 예제에서는 흔히 사용하는 두 가지 2차 방정식 함수인 (a) c1 = c2 = ½과 (b) c2 = c2 = 1을 선택했다. 선형 탐색처럼 계산 결과를 b개 저장소 중 하나에 맞게 정규화한다. keys2를 대상으로 다시 실험해보면 결과는 다음과 같다.
2차원 탐색(Quadratic probing)은 초기에는 선형 탐색보다 약간 비효율적이지만, 특정 교차점(배열이 현재 담은 원소 개수의 2배로 커질 때)을 지나면 성장률(growth rate)이 훨씬 좋아진다. 마지막 경우에서 2차원 탐색을 사용하면 선형 탐색보다 거의 5배 빠르다. 하지만 원소를 저장소에 효율적으로 분배하는 계수를 주의해 선택해야 한다. 예를 들어, c1 = c2 = 1일 때 결과는 선형 탐색에 더 가까우며, b = 658이라면 621개 슬롯만 채워지도록 허용하여, 622번째 단 어 삽입을 시도하면 적합한 빈 슬롯을 찾기 데 실패한다.
해시 기반 검색: 충돌 목록
해시 기반 검색에서는 해시 함수가 반환한 계산 값이 동일한 원소를 모두 저장하는 리스트를 만들어 충돌을 해결할 수 있다. JDK에서 제공하는 java.util.Hashtable 클래스에서 이 방식을 구현한다.
해시 테이블에 있는 원소의 개수가 특정 "부하율(load factor)"의 한계(threshold)를 넘어서면 해당 해시 테이블이 확장되고(일반적으로 크기 b가 2*b+1로 변경 된다), 저장된 원소들이 새 위치로 리해시된다(rehashed). 이렇게 확장된 해시 테이블이 리해시 메소드의 비용을 보상하여 (책의 [표 5-7]에 기술한 것처럼) 충 분한 비용 절감을 얻는다. 필자는 JDK에서 해시 테이블을 계산하는 방법에 대한 감을 얻을 수 있도록 n=641일 때 용량이 각각 {11, 4*n=2564, 4413}인 초기 해시 테이블을 사용해 원하는 키 원소로부터 해시 테이블을 채우는 세 가지 실험을 수행했다. 각 경우에서 해시 테이블을 만드는 데 드는 시간은 미미하다. 초 기 크기 11로 시작한 경우(641개 원소를 삽입한 후) 결과 해시 테이블이 리해싱으로 인해 1,535개 공간을 보유하게 됨을 주목하기 바란다. 표에 213,557개 단 어를 모두 조회하는 데 필요한 평균 검색 시간도 나타냈다.
실행 결과가 선형 탐색과 2차원 탐색보다 2배 가량 느리다. 왜 그럴까? java.util.Hashtable의 소스 코드를 살펴보면, 동일한 저장소로 해시되는 원소의 충돌을 연결 리스트를 사용해 해결함을 알 수 있다. 이는 해시 테이블에서 원소를 삭제할 수 있게 하므로 현실적인 해싱 해결책이다. 선형 탐색이나 2차원 탐색에 사 용하는 배열에서는 원소를 간편하게 삭제할 수 없다. 대신, 저장소를 삭제된 것으로 표시해 체인이 계속 처리되게 한다. 그러면 java.util.Hashtable에 있는 이들 연결 리스트의 평균 길이는 얼마나 될까? 이 클래스의 설계자들은 이 유용한 정보를 거의 얻을 수 없게 만들어 놓았다. 필자는 연결 리스트의 평균 길이 정보 를 얻기 위해 해시 테이블의 직렬화 가능 표현을 절묘하게 조작하는 HashtableReport라는 작은 클래스를 작성했다. 재치 있는 해결책이라는 생각이 들 것이다. 모든 상황에서 위의 표는 평균 체인 길이가 초기에 더 높음(약 30%)을 보여준다. 하지만 실험 3처럼 연결 리스트 길이가 더 작을 때조차 이들 연결 리스트를 순회하는 데 필요한 추가 계산으로 인해 성능 면에서 비효율적이다.
해시 기반 검색: 완전 해싱
완전 해시(perfect hash)는 집합을 표현하는 배열을 한 번 탐색해서 대상 단어의 존재 여부를 판별할 수 있게 해주는 해시 함수다. 무료로 얻을 수 있는 완전 해 싱용 소프트웨어 패키지가 몇 가지 있다. C 언어용을 예로 들면, GNU GPERF 패키지는 완전 해싱을 수행하는 C 코드를 생성한다. 가장 많이 차용되는 것은 더 글라스 슈미트(Doug Schmidt)의 완전 해시 생성기(Perfect Hash Generator) 며, GNU 사이트에서 코드를 얻을 수 있다.
완전 해시를 생성하려면, 미리 검색할 원소들의 집합 전체를 알아내야 하고, 대상 단어가 집합에 존재하면 해당 배열 위치를 알려줄 적합한 해시 함수를 설계 해야 한다. 완전 해싱의 가장 큰 약점은 집합을 표현하는 배열의 크기가 매우 크고 듬성듬성하다는 것이다. 예를 들면, 다음과 같다.
매우 큰 단어 집합인 경우에 이러한 접근법은 분명 비현실적이다. 완전 해싱의 두 번째 약점은 집합을 표현하는 배열의 생성 비용과 해시 함수의 검색 비용이 눈에 띄게 높다는 것이다. 예를 들어, 2기가헤르츠 칩을 보유한 듀얼코어 AMD 옵테론 프로세서(Opteron Processor)에서 GPERF는 keys3용 배열과 해시 함수 를 계산하는 데 약 2분 30초를 소비했다.
이 컬럼에서는 GPERF로 keys2와 keys3용 C 코드를 생성한 다음, 이를 수동으로 자바로 변환했다. 자바 컴파일러가 강제하는 몇몇 상수 풀링(constant pooling) 제약 때문에 GPerfThree 코드는 디스크에서 큰 배열을 로드해야 한다. 위의 표에서 keys3용 GPERF의 성능이 느려지는 것을 볼 수 있다. 이는 해당 해시 함수의 부가적인 복잡성 때문이다.
특수한 경우를 다루는 해싱
집합이 특수한 성질을 지니면, 완전 해싱에 사용할 효율적인 해시 함수를 손수 만들어낼 수 있다. 실제로 집합을 저장하는 데 사용하는 배열에 작은 여분의 저 장 공간을 요구하는 해시 함수를 만들 수 있기도 하다. GPerfTwo와 GPerfThree에 있는 해시 함수를 살펴보면, 고정 개수 문자로 구성된 문자열을 조사하는 데 기반을 두고 있음을 알 수 있다. 여기서는 keys2와 keys3 집합을 이루는 단어를 선택할 때 이 접근법을 극단적으로 활용한다. 자세히 설명하면 다음과 같다.
균형 이진 트리를 사용하여 집합 저장하기
이 컬럼에서 설명하는 해싱 접근을 단순히 균형 이진 트리를 사용하는 것과 비교할 가치가 있다. 이 코드는 BalancedTreeSearch에서 찾을 수 있다. 듬성듬성한 배열을 해시 테이블로 사용할 때 단순히 저장할 공간이 없으면, 총 "탐색" 횟수가 트리의 높이로 제한될 수 있기 때문에 균형 트리가 합리적인 해결법이 된다( 균형 이진 트리인 경우 O(log n)). 다음은 성능 측정 결과다.
트리의 깊이는 트리에 있는 원소를 찾는 데 사용할 수 있는 최대 "탐색" 횟수라는 점을 주목하기 바란다. 여기서는 트리에서 각 개별 원소를 찾는 데 필요한 평
균 탐색 횟수도 계산했다. 선형 탐색을 사용한 경우 keys2 집합의 평균 체인 크기가 11.90인 유일한 경우는 배열 크기 b=658일 때였으며, 평균 검색 시간은
40배 이상 느린 2,966.54였다.
유용한 해시코드 단축 생성 기교
hashCode 메소드에서 음수를 반환할 수 있으므로, 다음 코드 대신 책의 [예제 5.8]에서 사용한 유용한 기교를 사용할 수 있다.
이클립스 워크스페이스로 ADK 가져오기
ADK 파일을 다운로드해서 압축을 풀면, [그림 1]과 같이 ADK/Deployment를 루트로 하는 디렉토리 구조가 나타난다.
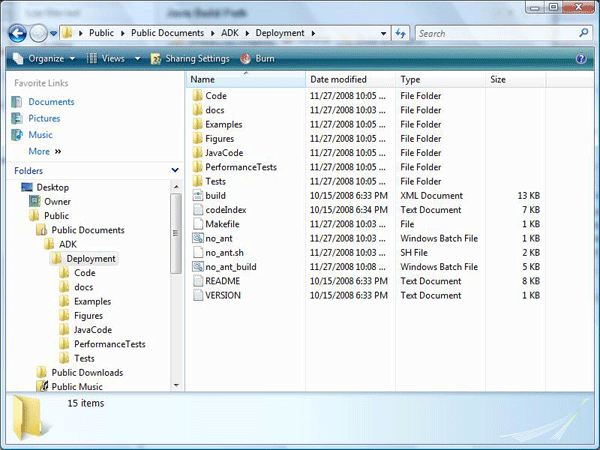
[그림 1] ADK 디렉토리 구조를 보여주는 탐색기 창
알고리즘의 자바 구현체에 접근하려면 해당 JavaCode 프로젝트를 이클립스로 임포트만 하면 된다. 이클립스 워크스페이스에서 New Java Project를 생성하면 [그림 2]와 같은 대화상자가 나온다.
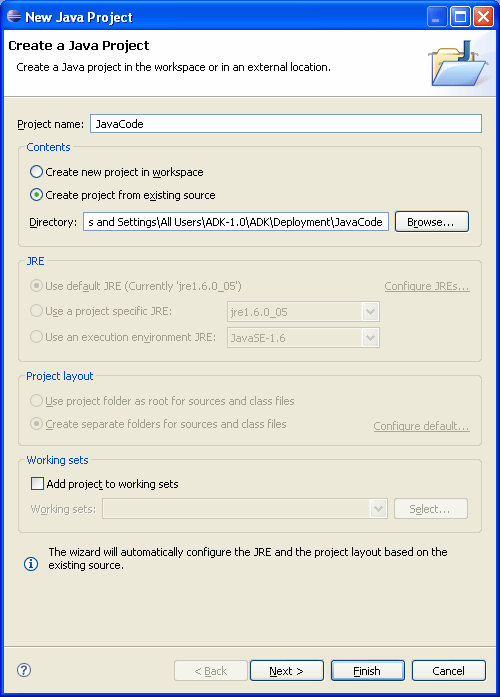
[그림 2] New Java Project 생성 대화상자
먼저 "Create project from existing source" 항목을 선택한다. 그리고 $ADKSHOME 디렉토리로 이동해 JavaCode 디렉토리를 선택하고 버튼을 클릭하면 코드가 임포트된다. 사용하는 머신에 JDK 1.6.0_05 버전이 설치되어 있지 않으면, JavaCode 프로젝트에서 올바른 JDK를 찾을 수 있도록 JRE 시스템 라이브러리를 설정해야 한다. 간단히 말하면, JavaCode 프로젝트의 빌드 경로를 편집해서 JRE 시스템 라이브러리를 설치된 버전과 연결한다. 이 작업을 수행하는 방법은 이클립스 문서를 참고하기 바란다.
이클립스 워크스페이스로 12월 코드 가져오기
이번 달 코드를 이클립스로 불러오려면, 먼저 code.zip(141,995바이트) 파일을 다운로드해서 압축을 푼다. 그런 다음, 이클립스 New Java Project 생성을 선택하면 [그림 2]와 같은 대화상자가 나타난다.
"Project name"란에 "December 2008"을 입력한다. "Create project from existing source" 항목을 선택하고 code.zip 파일의 압축을 푼 위치로 이동한다. 반드시 "December_2008" 디렉토리를 선택해야 한다. 마지막으로 버튼을 클릭한다. ADK에서 이 이클립스 워크스페이스로 JavaCode 프로젝트를 임포트하면 코드가 깔끔하게 컴파일되어야 한다. 그렇지 않으면, 이클립스 프로젝트에서 알고리즘 구현이 담긴 ADK의 컴파일된 Jar 파일 위치를 지정해야 한다.
이번 달 컬럼에 보인 모든 데이터를 생성한 메인 프로그램을 띄우려면, 새로운 실행 구성(run configuration)을 생성해야 한다. [Run] --> [Run Configurations...] 메뉴를 선택한 다음 새로운 런치 구성(launch configuration)을 생성한다. "Main class" 이름을 search.main.Main으로 설정하고 Arguments 탭에서 프로그램에 필요한 인자 세 개를 입력해야 한다. 첫 번째 인자는 ADK 설치 디렉토리를 기준으로 "words.english.txt" 파일의 위치, 나머지 두 인자는 각각 특수한 키 파일인 "keys_2.txt"와 "keys_3.txt"이다. 예를 들어, 다음은 필자가 설정한 화면이다.
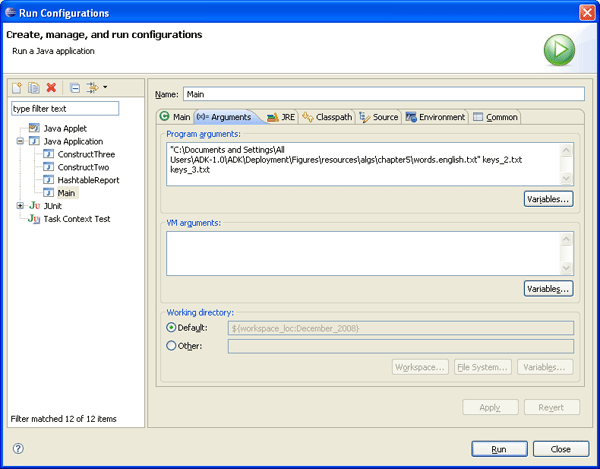
메인 프로그램은 인터넷에만 연결되어 있으면 오라일리 사 웹사이트에 자동으로 접속해 필요한 "words.english.txt" 파일(프로그램의 다음 실행을 위해 저장해둔다)을 다운로드하므로 간편하게 인자 없이 search.main.Main 클래스를 실행할 수 있다.
다음 컬럼
1월 컬럼에서는 ‘6장. 그래프 알고리즘’에 있는 알고리즘을 더 연구할 것이다. 그때까지 Algorithms in a Nutshell 책에 있는 다양한 알고리즘을 연구해보고, ADK에서 제공하는 예제를 살펴보기 바란다.
저자 : George T. Heineman
역자 : 한빛독자
원문 : December Column: Searching Algorithms
이 컬럼은 2008년 10월 오라일리에서 출간한 Algorithms in a Nutshell 관련 블로그에 연재된 월간 컬럼 시리즈의 두 번째 기사다.
지난 컬럼에서는 다음 내용을 다뤘다.
- 책 관련 코드 저장소인 알고리즘 개발 키트(ADK, Algorithm Development Kit)를 다운로드하고 설치하는 방법
- C 언어로 구현한 몇 가지 정렬(Sorting) 알고리즘을 사용하는 방법
- 11월 컬럼의 코드 샘플을 다운로드하는 방법
- 존재: 집합 C가 대상 원소 t를 포함하는가?
- 추출: 집합 C에서 대상 원소 t와 일치하는 원소 반환
- 관련 조회: 집합 C에서 대상 키 k와 연관된 정보 반환
12월 컬럼의 코드 샘플 다운로드
코드 샘플인 code.zip 파일(141,995바이트)은 이곳에서 다운 로드받을 수 있다. 예제는 윈도우에서 이클립스 3.4.1 버전으로 테스트하였고 JDK 버전은 1.6.0_05이다. code.zip 파일은 익스포트된 이클립스 프로젝트기 때문에 이클립스 워크스페이스로 쉽게 불러올 수 있다. 이클립스 외부에서 컴파일하고 실행하려면, CLASSPATH 환경 변수를 설정하여 컴파일된 ADK 소스를 사용하게 하면 된다.
코드를 이클립스로 임포트하는 방법은 컬럼 뒷부분을 참고하기 바란다.
검색 루틴용 API 인터페이스
다음 코드는 원소 집합에 특정 원소가 존재하는지 여부를 판단하는 API(이 블로그용으로 정의함)를 보여준다.
public interface ICollectionSearch이 인터페이스는 자바 제네릭스(generics)를 활용하여, 검색 가능한 집합을 해당 집합에 포함된 기본 원소의 타입에 따라 매개변수화될 수 있게 한다. 이 컬럼 에 있는 검색 알고리즘의 구현체는 ICollectionSearch 인터페이스를 구현하므로 직접 접근 방법을 비교할 수 있다. 이 컬럼에서는 다음 내용을 다룬다.{ /** * 전달받은 대상 원소가 집합에 있는지 판단한다. * @param target 널이 아닌 검색할 원소. * @return true - 대상 원소가 집합에 존재하는 경우. false - 존재하지 않는 경우. */ boolean exists(E target); }
- 해시 기반 검색: 선형 탐색, 2차원 탐색, 충돌 목록과 완전 해싱
- 균형 이진 트리 검색
- keys2 - 641개 단어 포함
- keys3 - 6,027개 단어 포함
구체적으로 표현하기 위해 검색할 대상 집합의 크기를 n이라고 한다. n개의 원소 각각의 키(key) 값을 계산할 수 있는데, 해시 기반 집합에서는 b개 저장소(슬 롯이라고도 한다)의 배열을 만든다.
순차 검색: 다소 아쉬운 알고리즘
해싱 연구의 목적은 순차 검색의 약점을 극복하기 위함이다. 집합이 정렬되어 있지 않으면 한 원소를 검색하는 데 최악의 경우 O(n)의 비용이 든다. 집합이 정 렬되어 있어도 원소가 고르게 배분되어 있으면 원소의 절반을 조사해야 하므로 비용은 여전히 O(n)이다.
해시 기반 검색: 선형 탐색
선형 탐색은 본질적으로 적은 탐색 횟수만으로 배열에 특정 원소가 존재하는지 여부를 판단할 수 있는 배열을 통해 집합 원소를 분산시킨다. 이를 위한 첫 번 째 방법은 b(저장소의 개수)가 n(원소의 개수)보다 클 수 있음을 인식하는 것이다. 해시 함수가 원소를 저장할 저장소를 계산하기 위해 원소의 키 값을 받고 보 통 나머지 연산자("%")를 사용해 b개 저장소 중 하나에 맞게 정규화한다. 정규화한 저장소 번호는 h라고 한다. 두 번째 방법은 계산된 저장소가 같은 원소가 둘 이상일 때 충돌을 해결하는 것이다. 선형 탐색(linear probing) 기법은 충돌을 해결하기 위해 열린 위치 지정(open addressing)을 사용하는데, 이는 insert(e) 메 소드에서 다른 저장소를 선택해 삽입 항목을 넣음을 의미한다. exists(e) 메소드는 이후에 대상 원소가 집합에 있는지 판단하기 위해 여러 저장소를 조사할 수 도 있다.
다음 메소드(첨부 코드에 있는 HashBasedSearch 클래스에서 발췌함)는 해시 테이블을 표현하는 배열에 원소를 삽입하는 로직이다. 빈 저장소를 찾는 데 탐색 한 횟수를 반환하며, 빈 저장소가 없으면 RuntimeException을 던진다. b가 소수(prime number)면, [1, b-1] 범위에 있는 모든 델타(delta)를 사용할 수 있다. 그 렇지 않으면 b와 delta의 최대 공약수(GCD, greatest common divisor), 즉 서로 소 값을 사용해야 한다.
/**
* storage[]로 표현한 집합에 원소를 삽입한다.
*
* 시도한 슬롯의 개수가 배열 크기에 도달하면
* 해시 함수가 빈약하거나 배열이 가득 차
* 원소를 추가할 수 없음을 선언한다
*
* 원소가 집합에 이미 있으면,
* 해당 집합을 변경하지 않고,
* 원소를 찾는 데 든 탐색 횟수를 반환한다.
*
* @param e 삽입할 원소
* @return 위치를 찾기 위해 탐색한 횟수
* @throws RuntimeException 주어진 delta 단계에서 빈 위치를 찾을 수 없는 경우
*/
public int insert(E e) throws RuntimeException {
// 초기 저장소 위치를 계산한다.
int hash = (e.hashCode() & 0x7FFFFFFF) % storage.length;
int h = hash;
for (int p = 1; p <= storage.length; p++) {
if (storage[h] == null) {
storage[h] = e;
num++;
return p;
} else if (storage[h].equals(e)) {
return p;
}
// 다음 저장소로 넘어간다.
h = probe.next(hash, p);
}
throw new RuntimeException ("Unable to insert element: " +
num + " slots taken out of " + storage.length);
}
LinearProbe 타입인 probe 객체는 각 탐색 시도에서 조사할 적합한 저장소를 계산한다. 선형 탐색에서는 계산된 저장소(h)가 이미 찬 경우, (h + p*delta) %
tableSize인 저장소를 선택해 충돌을 해결한다(여기서 delta는 미리 배정한 상수, p는 탐색 번호다). 예를 들어, delta가 "3"인 경우 배열에 원소를 삽입하려고
하면 수열 h, h+3, h+6, ..에서 첫 번째 빈 저장소에 넣는다. 이러한 모든 저장소 번호를 나머지 값 b로 계산하므로 배열을 환형 구조로 다루고, 원소를 배열에
올바르게 넣는 데 필요한 탐색 횟수를 기술하는 데 체인(chain)이라는 용어를 사용한다.
다음 표는 delta 값을 1로 유지하고, keys2에 해당하는 641개 문자열을 크기가 서로 다른 해시 테이블에 삽입한 결과다.
| 배열 크기 b | 비어 있는 저장소 | 평균 체인 크기 | 최대 체인 크기 | 평균 검색 시간(ms.) |
| 9,615 | 8,974 | 1.03 | 2 | 13.39 |
| 5,128 | 4,487 | 1.07 | 3 | 14.54 |
| 4,413 | 3,772 | 1.10 | 5 | 16.18 |
| 2,884 | 2,243 | 1.14 | 6 | 17.29 |
| 1,762 | 1,121 | 1.26 | 12 | 24.57 |
| 1,201 | 560 | 1.49 | 10 | 34.57 |
| 921 | 280 | 2.41 | 53 | 98.21 |
| 781 | 140 | 2.98 | 46 | 149.04 |
| 711 | 70 | 4.18 | 64 | 313.61 |
| 676 | 35 | 5.29 | 127 | 565.89 |
| 658 | 17 | 13.82 | 446 | 2966.54 |
저장소의 개수 b가 n에 가까워질수록 충돌 횟수가 증가한다. 213,557개 단어를 모두 조회하는 데 필요한 평균 시간을 계산하는 마지막 열에서 두드러진 현상 을 볼 수 있다. 평균 탐색 횟수가 적을 때는 O(n)의 탐색 횟수가 필요한 원소도 있어 사용자가 충분히 큰 배열을 사용해 일부 상황을 제어할 수 있다.
delta 값의 선택은 중요하지 않다. 4가지 특정 크기 배열에 서로 다른 delta 값을 적용한 결과를 보여주는 다음 표를 살펴보자.
| 테이블 크기: 641 | 테이블 크기: 1283 | 테이블 크기: 2557 | 테이블 크기: 5113 | |||||
| 델타 | 평균 | 최대 | 평균 | 최대 | 평균 | 최대 | 평균 | 최대 |
| 1 | 21.11 | 585 | 1.43 | 7 | 1.17 | 7 | 1.07 | 4 |
| 2 | 21.05 | 615 | 1.50 | 10 | 1.15 | 6 | 1.06 | 3 |
| 3 | 17.37 | 585 | 1.42 | 7 | 1.15 | 6 | 1.07 | 3 |
| 4 | 23.53 | 593 | 1.49 | 15 | 1.14 | 5 | 1.07 | 4 |
| 5 | 15.02 | 570 | 1.44 | 8 | 1.15 | 6 | 1.07 | 4 |
| 6 | 21.68 | 490 | 1.53 | 17 | 1.17 | 6 | 1.06 | 3 |
| 7 | 18.02 | 596 | 1.51 | 13 | 1.13 | 4 | 1.08 | 4 |
| 8 | 12.26 | 299 | 1.50 | 11 | 1.15 | 6 | 1.07 | 3 |
| 9 | 12.12 | 564 | 1.50 | 16 | 1.14 | 5 | 1.06 | 4 |
필자는 예상보다 약 4-8배 큰 배열을 선택할 것을 권한다. 크기가 그 정도는 되어야 총 탐색 횟수는 물론 각 항목을 찾는 데 사용되는 탐색 횟수의 변화가 줄기 때문이다. 해시 테이블 배열을 만들고 나면, 배열 안에서 최대 체인이 원소의 존재 여부를 평가하는 데 드는 시간을 결정한다. 여기서는 탐색 횟수를 줄이기 위 해 여분의 (사용하지 않은) 공간을 두는 트레이드 오프가 있다.
해시 기반 검색: 2차원 탐색
2차원 탐색은 선형 탐색을 사용할 때 발생하는 클러스터링을 피하려고 시도한다. 2차원 탐색은 ((int)(hash + c1*p + c2*p*p)) % tableSize 형태의 수식을 사용 해서 p번째 저장소를 계산한다(여기서 c1과 c2는 부동소수점 계수다). 이 컬럼의 예제에서는 흔히 사용하는 두 가지 2차 방정식 함수인 (a) c1 = c2 = ½과 (b) c2 = c2 = 1을 선택했다. 선형 탐색처럼 계산 결과를 b개 저장소 중 하나에 맞게 정규화한다. keys2를 대상으로 다시 실험해보면 결과는 다음과 같다.
| 평균 체인 크기 | 최대 체인 크기 | 평균 검색 시간(ms.) | |||||
| 배열 크기 b | 비어 있는 저장소 |
q1=½ q2 =½ |
q1=1 q2=1 |
q1=½ q2 =½ |
q1=1 q2=1 |
q1=½ q2 =½ |
q1=1 q2=1 |
| 9,615 | 8,974 | 1.03 | 1.03 | 2 | 3 | 13.93 | 13.43 |
| 5,128 | 4,487 | 1.08 | 1.07 | 4 | 4 | 15.07 | 15.07 |
| 4,413 | 3,772 | 1.09 | 1.08 | 4 | 3 | 15.65 | 15.61 |
| 2,884 | 2,243 | 1.14 | 1.12 | 4 | 3 | 17.89 | 17.29 |
| 1,762 | 1,121 | 1.26 | 1.26 | 8 | 8 | 24.00 | 24.00 |
| 1,201 | 560 | 1.45 | 1.44 | 8 | 9 | 35.18 | 34.61 |
| 921 | 280 | 1.89 | 1.86 | 13 | 16 | 57.46 | 59.71 |
| 781 | 140 | 2.16 | 2.26 | 19 | 24 | 90.93 | 89.29 |
| 711 | 70 | 2.63 | 2.89 | 30 | 44 | 169.61 | 163.5 |
| 676 | 35 | 3.24 | 3.33 | 51 | 74 | 277.93 | 498.32 |
| 658 | 17 | 4.07 | ** | 91 | ** | 574.21 | ** |
2차원 탐색(Quadratic probing)은 초기에는 선형 탐색보다 약간 비효율적이지만, 특정 교차점(배열이 현재 담은 원소 개수의 2배로 커질 때)을 지나면 성장률(growth rate)이 훨씬 좋아진다. 마지막 경우에서 2차원 탐색을 사용하면 선형 탐색보다 거의 5배 빠르다. 하지만 원소를 저장소에 효율적으로 분배하는 계수를 주의해 선택해야 한다. 예를 들어, c1 = c2 = 1일 때 결과는 선형 탐색에 더 가까우며, b = 658이라면 621개 슬롯만 채워지도록 허용하여, 622번째 단 어 삽입을 시도하면 적합한 빈 슬롯을 찾기 데 실패한다.
해시 기반 검색: 충돌 목록
해시 기반 검색에서는 해시 함수가 반환한 계산 값이 동일한 원소를 모두 저장하는 리스트를 만들어 충돌을 해결할 수 있다. JDK에서 제공하는 java.util.Hashtable 클래스에서 이 방식을 구현한다.
해시 테이블에 있는 원소의 개수가 특정 "부하율(load factor)"의 한계(threshold)를 넘어서면 해당 해시 테이블이 확장되고(일반적으로 크기 b가 2*b+1로 변경 된다), 저장된 원소들이 새 위치로 리해시된다(rehashed). 이렇게 확장된 해시 테이블이 리해시 메소드의 비용을 보상하여 (책의 [표 5-7]에 기술한 것처럼) 충 분한 비용 절감을 얻는다. 필자는 JDK에서 해시 테이블을 계산하는 방법에 대한 감을 얻을 수 있도록 n=641일 때 용량이 각각 {11, 4*n=2564, 4413}인 초기 해시 테이블을 사용해 원하는 키 원소로부터 해시 테이블을 채우는 세 가지 실험을 수행했다. 각 경우에서 해시 테이블을 만드는 데 드는 시간은 미미하다. 초 기 크기 11로 시작한 경우(641개 원소를 삽입한 후) 결과 해시 테이블이 리해싱으로 인해 1,535개 공간을 보유하게 됨을 주목하기 바란다. 표에 213,557개 단 어를 모두 조회하는 데 필요한 평균 검색 시간도 나타냈다.
| 선형 | 2차원 |
JDK 해시 테이블 실험 1 b=1,535 |
JDK 해시 테이블 실험 2 b=2,564 |
JDK 해시 테이블 실험 3 b=4,413 |
|
| 평균 체인 크기 | 1.10 | 1.09 | 1.21 | 1.13 | 1.08 |
| 평균 검색 시간(ms.) | 16.18 | 15.65 | 30.14 | 27.92 | 29.57 |
실행 결과가 선형 탐색과 2차원 탐색보다 2배 가량 느리다. 왜 그럴까? java.util.Hashtable의 소스 코드를 살펴보면, 동일한 저장소로 해시되는 원소의 충돌을 연결 리스트를 사용해 해결함을 알 수 있다. 이는 해시 테이블에서 원소를 삭제할 수 있게 하므로 현실적인 해싱 해결책이다. 선형 탐색이나 2차원 탐색에 사 용하는 배열에서는 원소를 간편하게 삭제할 수 없다. 대신, 저장소를 삭제된 것으로 표시해 체인이 계속 처리되게 한다. 그러면 java.util.Hashtable에 있는 이들 연결 리스트의 평균 길이는 얼마나 될까? 이 클래스의 설계자들은 이 유용한 정보를 거의 얻을 수 없게 만들어 놓았다. 필자는 연결 리스트의 평균 길이 정보 를 얻기 위해 해시 테이블의 직렬화 가능 표현을 절묘하게 조작하는 HashtableReport라는 작은 클래스를 작성했다. 재치 있는 해결책이라는 생각이 들 것이다. 모든 상황에서 위의 표는 평균 체인 길이가 초기에 더 높음(약 30%)을 보여준다. 하지만 실험 3처럼 연결 리스트 길이가 더 작을 때조차 이들 연결 리스트를 순회하는 데 필요한 추가 계산으로 인해 성능 면에서 비효율적이다.
해시 기반 검색: 완전 해싱
완전 해시(perfect hash)는 집합을 표현하는 배열을 한 번 탐색해서 대상 단어의 존재 여부를 판별할 수 있게 해주는 해시 함수다. 무료로 얻을 수 있는 완전 해 싱용 소프트웨어 패키지가 몇 가지 있다. C 언어용을 예로 들면, GNU GPERF 패키지는 완전 해싱을 수행하는 C 코드를 생성한다. 가장 많이 차용되는 것은 더 글라스 슈미트(Doug Schmidt)의 완전 해시 생성기(Perfect Hash Generator) 며, GNU 사이트에서 코드를 얻을 수 있다.
완전 해시를 생성하려면, 미리 검색할 원소들의 집합 전체를 알아내야 하고, 대상 단어가 집합에 존재하면 해당 배열 위치를 알려줄 적합한 해시 함수를 설계 해야 한다. 완전 해싱의 가장 큰 약점은 집합을 표현하는 배열의 크기가 매우 크고 듬성듬성하다는 것이다. 예를 들면, 다음과 같다.
| 키 목록 | 단어 개수 | 배열 크기 | 사용률 | 평균 검색 시간(ms.) |
| keys2 | 641 | 4,413 | 14.5% | 29.57 |
| keys3 | 6,027 | 264,240 | 2.3% | 39.04 |
매우 큰 단어 집합인 경우에 이러한 접근법은 분명 비현실적이다. 완전 해싱의 두 번째 약점은 집합을 표현하는 배열의 생성 비용과 해시 함수의 검색 비용이 눈에 띄게 높다는 것이다. 예를 들어, 2기가헤르츠 칩을 보유한 듀얼코어 AMD 옵테론 프로세서(Opteron Processor)에서 GPERF는 keys3용 배열과 해시 함수 를 계산하는 데 약 2분 30초를 소비했다.
이 컬럼에서는 GPERF로 keys2와 keys3용 C 코드를 생성한 다음, 이를 수동으로 자바로 변환했다. 자바 컴파일러가 강제하는 몇몇 상수 풀링(constant pooling) 제약 때문에 GPerfThree 코드는 디스크에서 큰 배열을 로드해야 한다. 위의 표에서 keys3용 GPERF의 성능이 느려지는 것을 볼 수 있다. 이는 해당 해시 함수의 부가적인 복잡성 때문이다.
특수한 경우를 다루는 해싱
집합이 특수한 성질을 지니면, 완전 해싱에 사용할 효율적인 해시 함수를 손수 만들어낼 수 있다. 실제로 집합을 저장하는 데 사용하는 배열에 작은 여분의 저 장 공간을 요구하는 해시 함수를 만들 수 있기도 하다. GPerfTwo와 GPerfThree에 있는 해시 함수를 살펴보면, 고정 개수 문자로 구성된 문자열을 조사하는 데 기반을 두고 있음을 알 수 있다. 여기서는 keys2와 keys3 집합을 이루는 단어를 선택할 때 이 접근법을 극단적으로 활용한다. 자세히 설명하면 다음과 같다.
- keys2 - 첫 번째와 마지막에서 두 번째 문자가 집합 안에서 유일한 단어 집합이다. 이 집합은 총 26 * 26 = 676개의 가능한 단어 중에서 641개를 포함한다 (94.8% 밀도).
- keys3 - 첫 번째, 가운데, 마지막에서 두 번째 문자가 집합 안에서 유일하다. 알파벳의 마지막 6개 글자는 자주 사용되지 않기 때문에, 여기서는 [a-t] 범위 에 있는 글자가 이 세 위치에 있는 단어만 선택했다. 이 집합은 총 20 * 20 * 20 = 8,000개의 가능한 단어 중에서 6,021개를 포함한다(75% 밀도).
public boolean exists(String t) {
int first = (int)(t.charAt(0)-"a");
int second = (int)(t.charAt(t.length()-2)-"a");
return target.equals(storage[first*26+second]);
}
필자는 이 특수한 집합용으로 641개 멤버 원소 각각을 구분하기 위한 효율적인 해시 함수를 설계했다. keys3용으로도 유사한 메소드를 작성했다. 이들 해시
함수는 이 컬럼에서 설명한 다른 범용 메소드의 성능을 모두 뛰어 넘는다. 이는 효율적인 알고리즘을 설계할 때 입력 집합에서 모든 특수한 문자를 이용해야
한다는 필자의 견해를 또 한번 재확인해주는 부분이다. 다음 표는 이들 특수 해시 함수의 성능을 보여준다.
| 키 목록 | 단어 개수 | 배열 크기 | 사용률 | 평균 검색 시간(ms.) |
| keys2 | 641 | 676 | 94.8% | 9.5 |
| keys3 | 6,027 | 8,000 | 75% | 16.21 |
균형 이진 트리를 사용하여 집합 저장하기
이 컬럼에서 설명하는 해싱 접근을 단순히 균형 이진 트리를 사용하는 것과 비교할 가치가 있다. 이 코드는 BalancedTreeSearch에서 찾을 수 있다. 듬성듬성한 배열을 해시 테이블로 사용할 때 단순히 저장할 공간이 없으면, 총 "탐색" 횟수가 트리의 높이로 제한될 수 있기 때문에 균형 트리가 합리적인 해결법이 된다( 균형 이진 트리인 경우 O(log n)). 다음은 성능 측정 결과다.
| 키 목록 | 평균 노드 높이 | 트리 높이 | 평균 검색 시간(ms.) |
| keys2 | 8.63 | 16 | 70.36 |
| keys3 | 11.90 | 22 | 117.21 |
유용한 해시코드 단축 생성 기교
hashCode 메소드에서 음수를 반환할 수 있으므로, 다음 코드 대신 책의 [예제 5.8]에서 사용한 유용한 기교를 사용할 수 있다.
int h = v.hashCode();
if (h < 0) { h = 0 - h; }
return h % tableSize;
위 문장을 다음과 같이 한 문장으로 바꿀 수 있다.
return (v.hashCode() & 0x7ffffffff) % tableSize;필자는 JDK의 java.util.Hashtable 소스 코드를 읽으면서 이 방법을 알게 됐다.
이클립스 워크스페이스로 ADK 가져오기
ADK 파일을 다운로드해서 압축을 풀면, [그림 1]과 같이 ADK/Deployment를 루트로 하는 디렉토리 구조가 나타난다.

[그림 1] ADK 디렉토리 구조를 보여주는 탐색기 창
알고리즘의 자바 구현체에 접근하려면 해당 JavaCode 프로젝트를 이클립스로 임포트만 하면 된다. 이클립스 워크스페이스에서 New Java Project를 생성하면 [그림 2]와 같은 대화상자가 나온다.

[그림 2] New Java Project 생성 대화상자
먼저 "Create project from existing source" 항목을 선택한다. 그리고 $ADKSHOME 디렉토리로 이동해 JavaCode 디렉토리를 선택하고
이클립스 워크스페이스로 12월 코드 가져오기
이번 달 코드를 이클립스로 불러오려면, 먼저 code.zip(141,995바이트) 파일을 다운로드해서 압축을 푼다. 그런 다음, 이클립스 New Java Project 생성을 선택하면 [그림 2]와 같은 대화상자가 나타난다.
"Project name"란에 "December 2008"을 입력한다. "Create project from existing source" 항목을 선택하고 code.zip 파일의 압축을 푼 위치로 이동한다. 반드시 "December_2008" 디렉토리를 선택해야 한다. 마지막으로

메인 프로그램은 인터넷에만 연결되어 있으면 오라일리 사 웹사이트에 자동으로 접속해 필요한 "words.english.txt" 파일(프로그램의 다음 실행을 위해 저장해둔다)을 다운로드하므로 간편하게 인자 없이 search.main.Main 클래스를 실행할 수 있다.
다음 컬럼
1월 컬럼에서는 ‘6장. 그래프 알고리즘’에 있는 알고리즘을 더 연구할 것이다. 그때까지 Algorithms in a Nutshell 책에 있는 다양한 알고리즘을 연구해보고, ADK에서 제공하는 예제를 살펴보기 바란다.
TAG :
최신 콘텐츠
